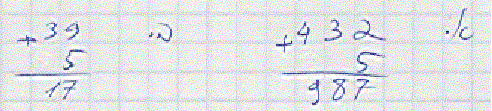
טעויות לדוגמה

תלמיד א פתר: 12 = 70+50 הסבר: "שבע ועוד חמש זה 12 ואפס זה כלום".

תלמיד ב פתר: 17 = 30+40 הסבר: "זה שבע עשרות וכך כותבים, שבע ועשר".

תלמיד ג פתר: 710 = 30+40 הסבר: "זה שבע עשרות וכותבים שבע עשרות, שבע ועשר".

תלמיד ד פתר: 70 = 30+40 הסבר: "עושים אפס ועוד אפס ושלוש ועוד ארבע".

שלושת התלמידים (א,ב,ג) לא ענו תשובה נכונה, אולם הקשבה להסבר שהם נותנים מצביעה על כך שיש הבדל רב בין תשובותיהם של התלמידים.הקשבה להסבר של תלמיד ד, שפתר נכון, מציבה אף היא שאלה, האם פתר מתוך הבנה.

תלמיד א חיבר נכון 7 ועוד 5 אך לא ייחס להם את ערך במקום. התלמיד לא התייחס למשמעות של האפס בספרת האחדות ולכן רשם את התשובה שקיבל מבלי להתייחס לערך המקום. כלומר, מההסבר שנתן עולה שהוא לא פועל מתוך הבנת ההיבט הכמותי של המספר ומתוך הבנה של המבנה העשרוני של המספרים ויתכן שהוא אינו מבין את הביטוי החשבוני שלפניו.יש לשים לב לכך שתלמיד א לא הסביר את דרך הכתיבה אלא תיאר את המהלך האלגוריתמי (פרוצדורה) שביצע

תלמיד ב ותלמיד ג מתייחסים אל ערך המקום ומחבר 3 עשרות ועוד 4 עשרות = ל- 7 עשרות אך מתקשים בשלב הכתיבה. הם מתרגמים ישירות את מה שאמרו – "שבע עשרות" לסמלים גרפיים ולא כותבים על פי ערך המקום. יתכן שהתלמידים מבינים את המספר בהיבט הכמותי שלו ובמקרה זה נאמר שהקושי הוא בשלב התרגום מהייצוג המילולי של המספר לייצוג הגרפי במספרים.

שגיאה דומה מופיעה בספרו של קרל לואיס "עליזה בארץ הפלאות" 4X5=12 – "שתי עשרות".

תלמיד ד מתאר את הדרך בה פתר אך מתוך המושגים והשפה המתמטית בה השתמש יש ספק אם הבין את ערך המקום ואת משמעות הפרוצדורה בה השתמש.

דרכי טיפול

תלמיד א
ניתן להניח שתלמיד זה מתייחס אל המספר כסמל גרפי בלבד ולא מעניק לו משמעות כמותית ולכן יש לחזק אצלו את ההבנה הכמותית של המספר הדו-ספרתי ובמיוחד של מספר הרשום כעשרות שלמות. בשלב ראשון ניתן לפעול בדרך של אימות לוגי, לבקש מהתלמיד לבצע אומדן ולהמחיש מילולית (בעזרת סיפור חשבוני או המללה של הכתוב לפניו) או/ו בעזרים, את הכתוב בתרגיל. יש לבקש מהתלמיד להשוות בין הביטויים 7+5 ו 70+50 ולשוחח על ההבדל הכמותי שבין שני הביטויים. במקרה זה יהיה נכון להמחיש את המספר הכתוב בעזרת עזרים מובנים (בדידי כוח עשר, גפרורים מאוגדים ואצל תלמיד מכיתה ג ואילף אף לשוחח על מטבעות כסף). חשוב לשוחח על ההבדלים בין המספרים ודרך כתיבתם.

תלמיד ב ותלמיד ג

יש לגשר בין הייצוג המילולי של המספר ודרך הכתיבה באופן גרפי תוך התייחסות לערך המקום. גישור כזה יכול להתבצע על ידי קישור לייצוג הכמותי-מוחשי של המספר.
לדוגמה: נבקש מתלמיד ב לקרוא את תשובתו (לדוגמה 17) ולהמחיש את הכמות, בעזרת אמצעי המחשה: קשיות מאוגדות לחבילות של 10 את התשובה. ניעזר בטבלת מראי מקום (טבלת אבקוס או כפי שמכנים אותה לעתים "בית המספרים"), ונבקש שיימקם את הכמויות ולאחר מכן את המספרים במקום המתאים בטבלה. כך ניצור קשר בין הייצוג המילולי, הגרפי והכמותי של המספר.

תלמיד ד

חשוב לבקש שימחיש את התרגיל ויסביר. ניתן לכוון אותו לשימוש במושגים מתמטיים (אחדות, עשרות) ולבדוק האם הוא מבין אותם ואת ערך המספר.

התלמיד חיבר את המספרים מבלי להתייחס לערך המקום של הספרות.
בתרגיל א: חיבר את 5 לאחדות, לעשרות וגם למאות, יתכן בשל הכללת יתר של תהליך כפל מאונך לתהליך של חיבור מאונך.
בתרגיל ב: חיבר את כל הספרות כתרגיל 9+5+3.

ממה נובעת הטעות

1. חוסר הבנה של משמעות תהליך החיבור של מספרים רב-סיפרתיים.
2. חוסר הבנה של המבנה העשורי: מבנה המספר וערך המקום.
3. חוסר הבנה כמותית של התוצאה ביחס למחוברים.

דרכי טיפול

• נלווה את הפעילות בחיזוק הבנת מבנה המספר התלת-ספרתי על ידי הפרדת המספר למחבריו, לדוגמה: 400+30+2=432, או על ידי קריאת המספר 432 כ- "4 מאות, 3 עשרות ו 2 אחדות".
• נלווה את הפעילות בחישוב בע"פ ובכתב בצרוף הכינויים של שם המקום, לדוגמה: "תחילה אני מחבר אחדות: 9 אחדות ועוד 5 אחדות ואחר כך אני מחבר את העשרות: 3 עשרות ועוד 0 עשרות…"
• נכתוב את התרגיל בתוך טבלת מקומות:

ממה נובעת הטעות?

1. זכירה חלקית של הפרוצדורה – התלמיד שכח לבצע את  ההמרה (ההעברה).
2. חוסר הבנה של המבנה העשורי בהתייחס לערך המקום ולפעולת ההעברה כמותית של התוצאה ביחס למחוברים.

הצעות לטיפול

1. במקרה שהתלמיד שכח לבצע את ההעברה, יש לתת לו רמזים מילוליים או תמרור לאיזכור קודם התחלת הפעולה, לדוגמ: מכינים מקרטון תמרור עצור שעליו כתוב: "שים לב, אל תשכח להעביר", ומניחים אותו לפני התלמיד.
2. במקרה של חוסר הבנה, יש להבהיר תחילה מושגים מתוך המבנה העשורי: איגוד, המרה, העברה, פריטה. יש לחזור ולהציג את נוהל החישוב (הפרוצדורה) בצמוד לטבלת מראי מקום, תוך הדגמה בקודים מילוליים וקונקרטיים כגון: "השלם לעשרת" "אגד עשרה גפרורים בגומייה", "המר עשר אחדות לעשרת אחת", "העבר עשרת אחת למקום העשרוני" ועוד.כדי לפתח את ערנות התלמיד למצבים בהם נדרשת העברה, ניתן לתת לו דף תרגילים שעליו יש לסמן (ולא לפתור) רק את אותם תרגילים שבהם יש לבצע העברה.

0.08 < 0.8

9.70 < 9.7

התלמיד ראה שבמספר יש מאיות ולכן קבע שהמספר קטן יותר.

ממה נובעת הטעות?

ניתן לשער שטעותו נבעה מהכללת יתר של הקשר בין המושגים "עשיריות" ו"מאיות". התלמיד הכיר את הכלל האומר שספרת המאיות קטנה מספרת העשיריות ומכך הסיק שמספר שיש בו מאיות קטן יותר ממספר שיש בו עשיריות.

דרכי טיפול

• התמקדות בחיזוק משמעות כמותית של שבר עשרוני.
• ליווי הפעילות בקריאת הנתונים בתוספת כינוייהם ובשאלות כגון: "כמה מאיות במספר 0.80?", "כמה עשיריות במספר 0.80?", ו"כמה עשיריות וכמה מאיות במספר 0.8?" ולהוביל את התלמיד למסקנה ש 8 עשיריות זהה ל 80 מאיות. לכן ניתן לקרוא את 9.7 ואת 9.70 כתשע ושבע עשיריות או כתשע ו 70 מאיות.
• הבלטת ערך המקום על ידי רישום הנתונים בטבלת מראי מקום (ניתן לחזק משמעות ערך המקום על ידי הוספת אפס בטור המאיות).
• המחשה באמצעים שונים כגון כסף: "9 שקלים ו 7 מטבעות של 10 אגורות" (1/10 השקל) לעומת, "9 שקלים ו-7 אגורות".
• כדי לחזק את ההבנה ניתן לבקש מהתלמיד להציב ספרות כדי ליצור מצבי שוויון או אי-שיוויון אחדים. לדוגמה: _ _ .4 < 4.32.

0.08 = 0.8
9.70 > 9.7

התלמיד התעלם מהנקודה ולפיכך השווה את המספרים לפי החלק שמימין לנקודה (70 לעומת 7) או לכל הספרות כמספרים ללא הנקודה (970 לעומת 97).

ממה נובעת הטעות?

3.85
7.29 +
1.114

ממה נובעת הטעות?

התלמיד ביצע נוהל חישוב על פי פרוצדורת חיבור אך התחיל מצד שמאל. ניתן לשער שטעותו נבעה מהתייחסות יתר לספרת השלמים במספר.

• התלמיד מתייחס אל המספרים כסמלים בלבד, מבלי לתת להם משמעות וערך למקום.
• התלמיד אינו מבין משמעות חיבור עם העברה ואינו מבין את משמעות פרוצדורת החישוב בחיבור עם העברה.

הערה: יש לבדוק תחילה כיצד פועל בחיבור בשלמים והאם מבין את הפרוצדורה בשלמים. במקרה שהתלמיד פועל באופן דומה בשלמים יש להתייחס כמו בשגיאה מספר 1 ושגיאה מספר 2

דרכי טיפול

ההצעות הבאות מתאימות למקרה בו הילד מבין את ערך המקום בשלמים אבל מיישם באופן שגוי אלגוריתם בחיבור בשברים בלבד.

• חשוב להבליט את הקשר בין רצף נוהלי החישוב אותם מבצעים לבין משמעות הפעולה של המרה וההעברה. כלומר, בין העובדה ש"מתחילים ממקום האחדות" לבצוע "העברה" ולאמירה "רושמים למעלה". לשם כך ניתן לערוך אנלוגיה בין מודל הפתרון האלגוריתמי בשלמים למודל הפתרון בשברים.
• להבליט את רצף נוהל החישוב ואת המשמעות של רצף זה תוך התייחסות לערך המקום בעל פה ובטבלת מראי מקום.
• במידת הצורך ניתן להמחיש בטבלה בכסף, או להשתמש בכינויי כסף.
• חשוב לעמת את הלומד עם תשובתו ולבקש תחילה לקרוא את התרגיל ואת התשובה, בתוספת כינויים (אגורות, שקלים), ולבחון האם התשובה הגיונית.

לפניך תרגיל: = 387+99
דני : התוצאה היא 312 כי 2 = 9-7 ; 1= 9-8 ; ומורידים את ה-3….".
המורה: הצע דרכים נוספות לחישוב בעל פה. שים לב למספרים . המספר 99 קרוב?
דני:אני לא יכול לעשות את התרגיל בלי לחשב במחשבון. אני חייב מחשבון.
דני לא מצליח לחשב בעל פה מתוך אומדן ומתוך קריאה של הרמזים המופיעים בטקסט המתמטי שלפניו. עבור דני חישוב משמעו ביצוע פרוצדורה כלשהי. כאשר הוא מתקשה הוא אינו יודע לבקר את המהלך שביצע ופונה למחשבון ש"יחלץ" אותו מהבעיה אליה נקלע.

דני אינו מבצע אומדן, אינו קורא נתונים מתוך הבנה כמותית ואינו מייעל את החישוב אלא צמוד לפרוצדורת החישוב אותה הוא לא מבין ולכן לא יודע ליישם ולפתור בלי עזרת המחשבון.

מה נעשה?

חשוב מאוד לחשוף את דני למשמעות הטקסטים המתמטיים והמשמעות הכמותית שלהם. חשוב לדבר עם דני על דרכים יעילות לחישוב ולהפנות את תשומת ליבו לכך שמספרים אינם סמלים בלבד אלא הם ברי משמעות כמותית. כדי להקל את דני להבין את המשמעות הכמותית ניתן להוריד את תחום המספר ולחזק את ההבנה של המבנה העשרוני כבסיס לחישוב יעיל. חשוב "להוכיח" לדני שקל יותר לחשב כאשר המספרים הם בחזקות של 10. במקרה זה לדוגמה, אם היה כתוב 387+100 היתה הפתרון קל יותר ולכן אם רשום "רק" 99, עליו להוריד 1. חשוב לנהל שיח מתמטי אודות הקשר בין מספרים למשמעות וללמד את דני להעניק משמעות למספרים שהוא קורא.